Research & Development Center
Research & Development Unit
YANMAR Technical Review
Improvement for Working Space Comfort (Prediction of Tractor Vibration)
Abstract
It is important to predict noise and vibration for the comfort of tractor driver.
In this study, we are focus on the tractor vibration of on-road running.
First, the phenomena of the vibration is investigated, it is influenced by the tire natural modes. Next, a tire is modeled by rigid ring, which could adopt roughness of road surface and lug excitation.
The dynamic characteristics of tire were measured by tire drum test machine, which was made by National Institute of Technology, Ube Collage.
The tire rigid ring model was used to calculate the excitation force from the tire lugs.
We confirmed the model can calculate the phenomena about the influence of tire natural modes.
1. Introduction
Yanmar is continually working on ways to improve tractor working space comfort by reducing vibration and noise. In particular, given the tendency for faster speeds when traveling on paved roads, Yanmar sees scope for investigate the mechanisms of traveling vibration and developing prediction techniques.
This article describes the mechanisms by which vibration occurs and the development of a tire model for predicting the amount of vibration.
2. Traveling Vibration
2.1. How to Represent Vibration
The physical quantities used to represent vibration are its amplitude (amount), phase (delay relative to a reference waveform), and frequency (number of cycles per second). Similarly, the determining factors for vibration are its source (excitation force) and transmission ( transfer system).
An important parameter for the transfer system is the natural frequency. All objects have a “natural frequency” at which they are easy to vibrate. The presence of an input (source of vibration) at this frequency will cause the object to resonate, resulting in large vibrations.
2.2. Vibration of Tractor when Traveling
Fig. 1 shows the measured vibration of a tractor as its speed is gradually increased. The measurements show an increase in vibration for the moment in the medium speed range, which decreases for a time before increasing again. In other words, vibration does not increase in proportion to traveling speed.
Fig. 2 shows a contour diagram of a frequency analysis of the vibration waveform. The vertical axis represents tractor speed, the horizontal axis represents frequency, and the color indicates amplitude. The diagram shows a particular frequency in the low-frequency region where vibration has a tendency to increase and decrease at different tractor speeds. This vibration is due to the natural frequency of the “mass-spring system” whereby inputs such as unevenness in the road cause the tires to act like springs and the tractor body to act as a vibrating mass. The diagram also shows inclined lines of higher vibration amplitude (bottom left to top right direction). These show increasing excitation frequency with increasing tractor speed, with the respective inclined lines corresponding to the frequency of the rear tire tread lug, the frequency of the front tire tread lug, and double the frequency of the rear tire tread lug (second order component).
Tractor tires differ from car tires in having large tread lugs (as shown in Fig. 3) to provide a good traction force when working on soil. The contact between the tread lug and the road surface provides the excitation force for the vibration.
The following equation expresses the frequency of the excitation force (primary component) caused by this contact between tire tread lug and the road surface, where v is the tractor speed (km/h), d is the tire diameter (m), L is the number of tread lugs per tire
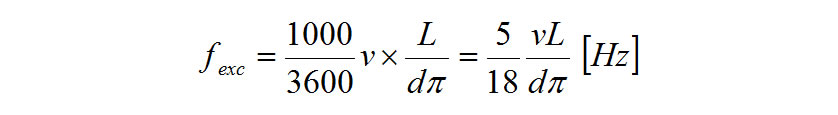
Substituting typical values for these variables (L=15, d=1.2 m), the equation gives (Hz), in which case the tractor speed (km/h) is roughly equal to the frequency of excitation of the tread lugs (Hz). This provides a simple intuitive understanding of what is happening.
(Hz), in which case the tractor speed (km/h) is roughly equal to the frequency of excitation of the tread lugs (Hz). This provides a simple intuitive understanding of what is happening.
In regard to the frequency of excitation due to the tread lug in Fig. 2, there is an increase in amplitude in the medium speed range, and it can be expected that this is the influence of some form of resonance.
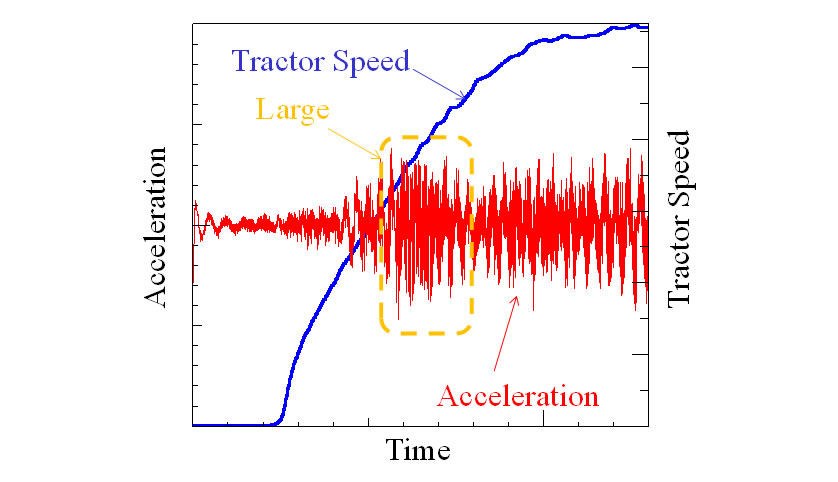
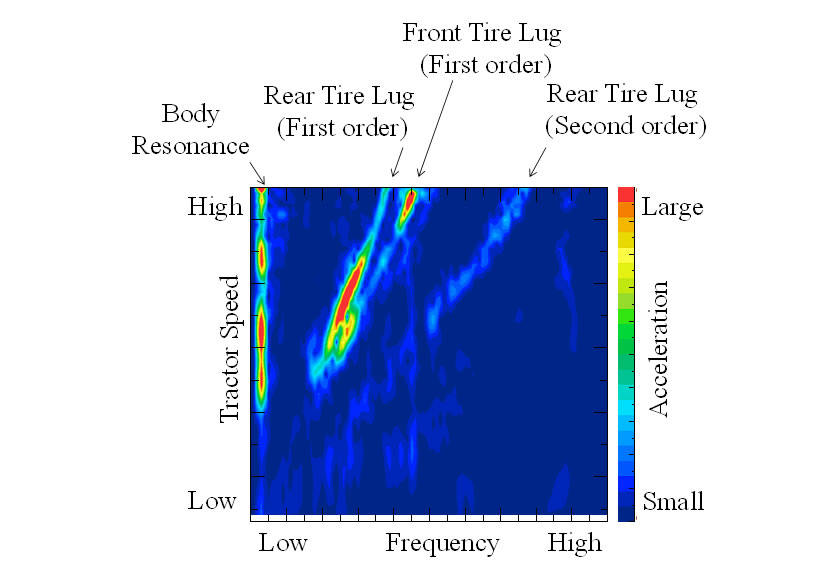

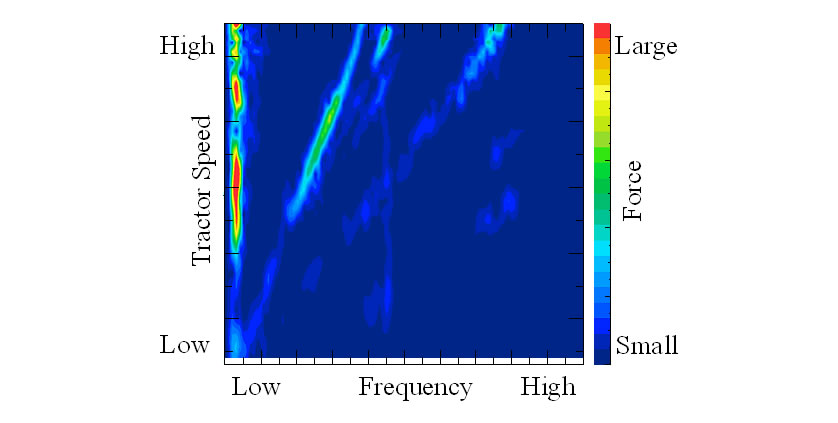
Fig. 4 shows a frequency analysis of the vibration input to the axle. This also shows that the excitation forces vary in the same way as the vibration itself. In other words, vibration is generated by the contact between the tread lug and the road surface, and this input increases or decreases as it transfers to the axle.
Between the road and axle are the tires, and resonance of the tires due to their natural vibration transmits a large excitation force to the axle.
2.3. Natural Vibration Modes of Tire
Fig. 5 shows an example of the natural vibration modes for a tire, obtained by FEM analysis. As tractor tires are heavier and larger than car tires and have a larger volume of rubber, they have a large number of vibration modes starting from comparatively low frequencies. The influence of these vibration modes can cause the vibration input to the axle to increase or decrease.
Vibration can be predicted by estimating the natural modes and calculating the response. However, tires have a complex internal structure, making it difficult to grasp their relevant physical properties. Accordingly, vibration prediction for tractors requires the development of a relatively simple model applicable to a restricted range of cases, and the identification of the appropriate inputs for the model. However, because the tires have a number of natural modes in the low-frequency range, as shown in Fig. 5, it is necessary to consider inputs from at least three directions.

3. Identifying Inputs Using Rigid Ring Model
For the first stage of model development, the model shown in Fig. 6 was created based on the rigid ring model proposed by Hans B. Pacejka. This is a simple model that considers the tractor body as a mass-spring system and can consider inputs from a number of different axes. This model can be used to consider the axial force that acts on the center of the wheel and the tread excitation force that acts on the point of contact with the road surface. However, the input from the point of contact with the road is restricted to two axes directions (vertical and longitudinal directions). Inputs of lateral direction to the axle cannot be considered.
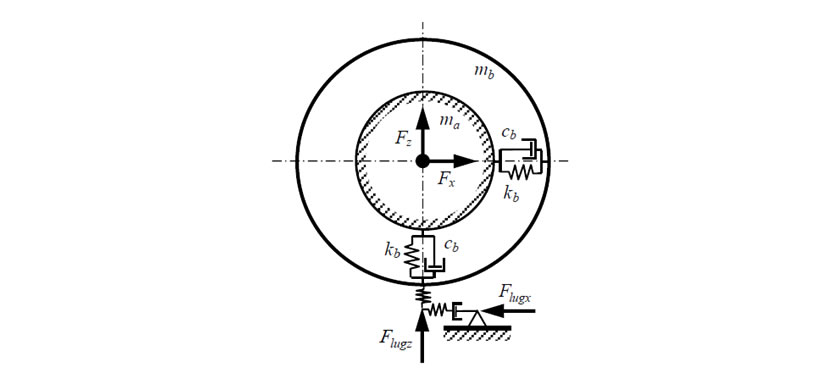
The motion equation for the rigid ring model is as follows.
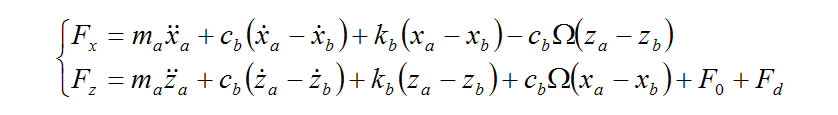
The forces (inputs) on the tread lugs are as follows,
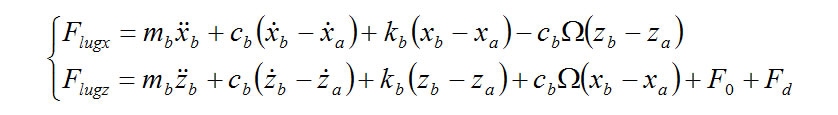
where:
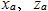 :Wheel displacement
:Wheel displacement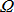 :Rotational velocity
:Rotational velocity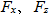 :Axial forces
:Axial forces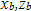 :Tire rim displacement
:Tire rim displacement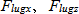 :Excitation force on tread lugs
:Excitation force on tread lugs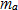 :Mass of wheel
:Mass of wheel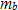 :Mass of tire ring
:Mass of tire ring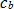 :side wall damping coefficient
:side wall damping coefficient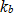 :side wall stiffness
:side wall stiffness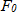 :Preload (static load)
:Preload (static load)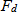 :Dynamic load
:Dynamic load
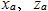 ,
, 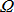 ,
, 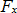 , and
, and 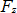 are measured using the experimental test bed described in section 4,
are measured using the experimental test bed described in section 4, 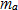 and
and 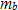 are actual measured values, and
are actual measured values, and 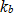 is determined from the displacement under static load. The value of
is determined from the displacement under static load. The value of 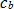 was estimated from past papers. The static load is the pressing force prior to running rotation tests and the dynamic load is the correction to the static load due to rotation.
was estimated from past papers. The static load is the pressing force prior to running rotation tests and the dynamic load is the correction to the static load due to rotation.
The variable component due to the excitation force from the tread lug is expressed by the following equation, considering components up to the fourth order.
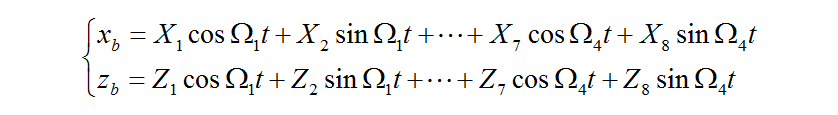
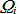 is the
is the 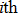 order component of the tread lug excitation frequency. By identifying the 17 unknowns (
order component of the tread lug excitation frequency. By identifying the 17 unknowns (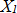 to
to 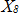 ,
, 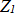 to
to 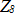 and
and 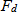 ), the inputs to the tread lugs (
), the inputs to the tread lugs (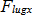 and
and 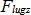 ) can be calculated. This identification is performed using the least-squares method to minimize the residual sum of squares.
) can be calculated. This identification is performed using the least-squares method to minimize the residual sum of squares.
The residual sum of squares is determined from the axle load measurements results and calculation results, as follows.
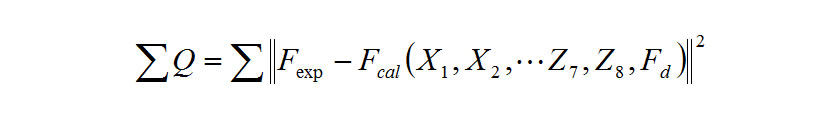
The partial differential equations for minimizing the residual are as follows.
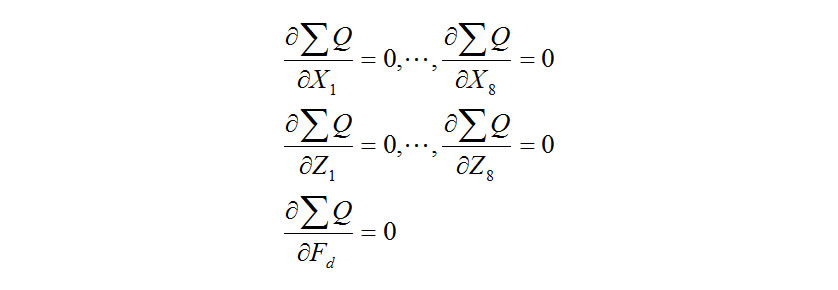
As these equations provide a set of simultaneous equations in the 17 unknowns, solving them makes it possible to identify the parameters.
4. Identifying Inputs Based on Drum Test
The drum test bed shown in Fig. 7 (which works by rotating the tire on a drum) was built (by the National Institute of Technology, Ube College) to identify excitation forces assuming the rigid ring model. However, because of the difficulty of handling large tractor tires, the test bed was designed to use small cultivator tires with a similar tread lug instead.
Fig. 8 shows the tread lug excitation force obtained by testing. This shows that the eigenvalue of the tire affect where the excitation force is large, and a good identification result was obtained that takes account of the excitation force due to the tread lugs adding tire transfer system.
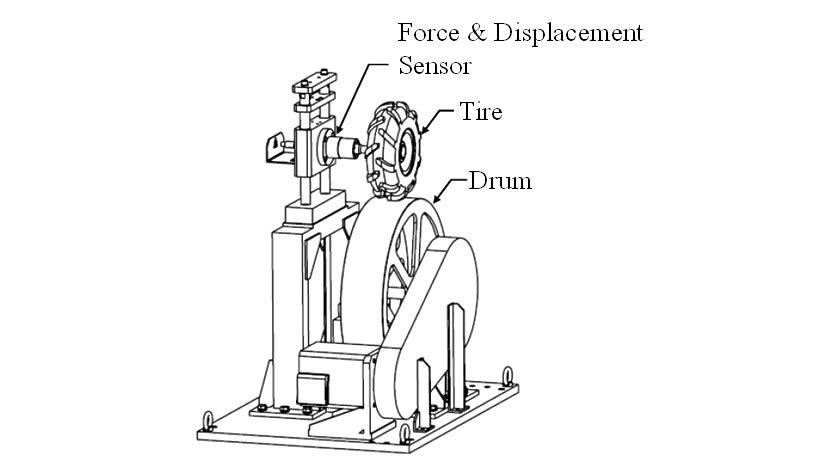
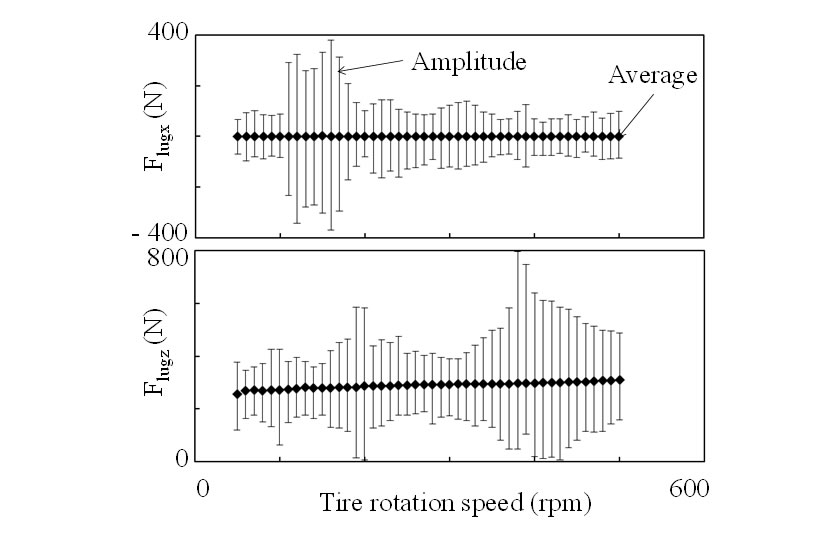
This model can be used to consider the two different inputs associated with road contact (unevenness on the road and tread lugs), and is expected to improve vibration prediction accuracy.
5. Conclusions
This work clearly shows that the natural modes of tire vibration can increase or decrease the level of tractor vibration when traveling on paved roads.
A mathematical formula was developed that can calculate the vibration inputs to the axles, including the influence of natural modes, using a rigid ring tire model.
The vibration inputs due to the contact between the tread lug and road surface were calculated based on experimental tests using small tires.
This has created a tire model that can consider the two main inputs (unevenness on the road and tread lugs).
In the future, Yanmar intends to improve tractor work space comfort by making further improvements to vibration prediction accuracy through improved parameter identification and by working on modelling capable of lateral inputs.
6. Acknowledgements
The development of this technology was cooperated by Professor Takashi Saito from the Division of Systems and Design Engineering, Graduate School of Science and Engineering, Yamaguchi University, and by Professor Katsuhide Fujita of the Department of Mechanical Engineering, National Institute of Technology, Ube College. The authors would like to take this opportunity to express their sincere thanks.
7. References
- (1)Hans B. Pacejka, ”Tyre and Vehicle Dynamics, Second Edition”, Elsevier (2006)
- (2)Zegelar, P.W.A. ”The dynamic response of tyres to break torque vibrations and road unevennesses”, PhD thesis, Delft University of Technology (1998)
- (3)Takanari Saguchi, “Influence of the Rolling Condition given to the Natural Frequency of a Tire”, Proceedings of Society of Automotive Engineers of Japan Symposium, Paper-No. 9840829, pp. 25-28 (1998) in Japanese
- (4)Noriyuki Fukuoka, “Vibration Characteristics of Tire”, Automotive Technology, Vol. 30 - No. 3, pp. 196-202 (1976) in Japanese
- (5)J.A.Lines, K.Murphy, “The Radial Damping of Agricultural Tractor Tyres”, Journal of Terramechanics, Vol. 29 - No. 02, pp. 207-221 (1992)
- (6)A. Kising, H.Gohlich, “Dynamic Eigenschaften von Traktor-Reifen”, J. Agric. Engng. Res., 43, pp. 11-21 (1989)
- (7)Committee for Preparation of Tire Design Guideline, “Offroad Tire Engineering –Fundamentals of Design and Performance Prediction-“, The Japanese Society for Terramechanics, pp. 221-222 (1999) in Japanese
- (8)Nobuya Yoshimura, Masahiro Takayama, “Vibrational Characteristics and Design Principle of a Tire,” Journal of the Japan Society of Mechanical Engineers, 88-805, pp. 1383-1389 (1985) in Japanese
- (9)Katsuhide Fujita, Takashi Saito, Mitsugu Kaneko, “Parameter Identification of an Agricultural Tire Considering Tire Lugs”, Transactions of the Japan Society of Mechanical Engineers, C, Vol. 73, No. 733, pp. 2479-2484 (2007) in Japanese
- (10)Katsuhide Fujita, Takashi Saito, Mitsugu Kaneko, “Study on dynamic characteristics of a rolling agricultural tire (Improvement of running condition)”, Transactions of the Japan Society of Mechanical Engineers, Vol. 80,No. 812 (2014) in Japanese
- (11)Katsuhide Fujita, Takashi Saito, Mitsugu Kaneko, “Influence of Vibration Characteristics on Dynamic Behavior of Rolling Agricultural Tire”, Journal of the Japanese Society of Agricultural Machinery, Vol. 37, No. 1, pp. 45-50 (2011) in Japanese
- (12)Katsuhide Fujita, Takashi Saito, Mitsugu Kaneko, “Study on Dynamic Characteristics of a Rolling Agricultural Tire”, Proceedings of 2015 Spring Conference of Society of Automotive Engineers of Japan, No. 40-15, pp. 964-968 (2015) in Japanese
-IMPORTANT-
The original technical report is written in Japanese.
This document was translated by R&D Management Division.


